Note: This post is part of a series on developing resmack. See the resmack tag for all posts in the series.

← Part 3 Perf Event Performance Overhead Part 5 Grammar Mutation and Recursion →

Fuzzing and Mutations

Feedback-driven fuzzing uses a form of genetic algorithm to generate inputs that ideally cause more and more more of the target program to be executed.

Genetic algorithms:

• Have a collection of inputs
• Create new inputs from previous inputs (mutate, crossover)
• Have a fitness function to determine the “success” of an input

The corpus of inputs used during fuzzing is the collection of inputs. The creation of new inputs is the mutating of items within the corpus to create new inputs. The feedback in feedback-driven fuzzing is often the fitness function.

Feedback-driven Grammar Fuzzing

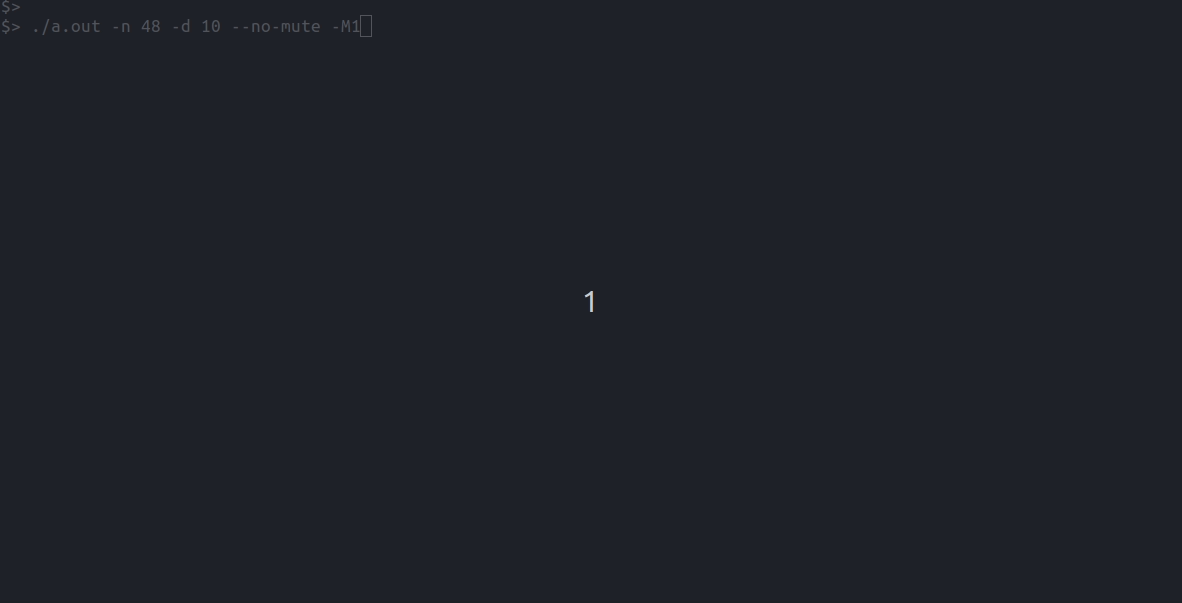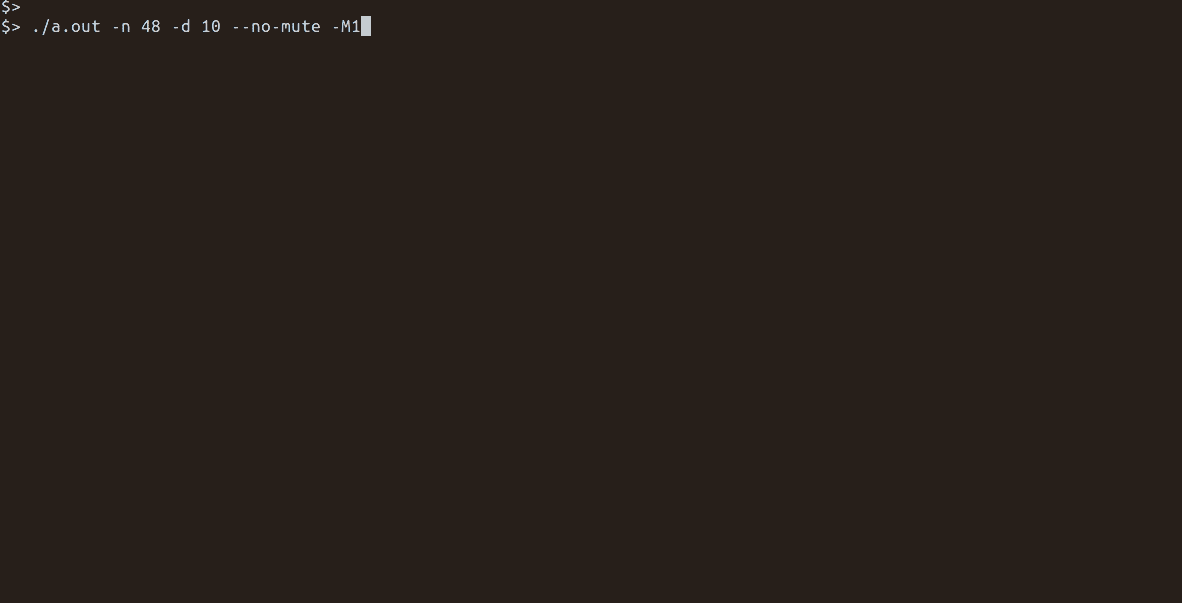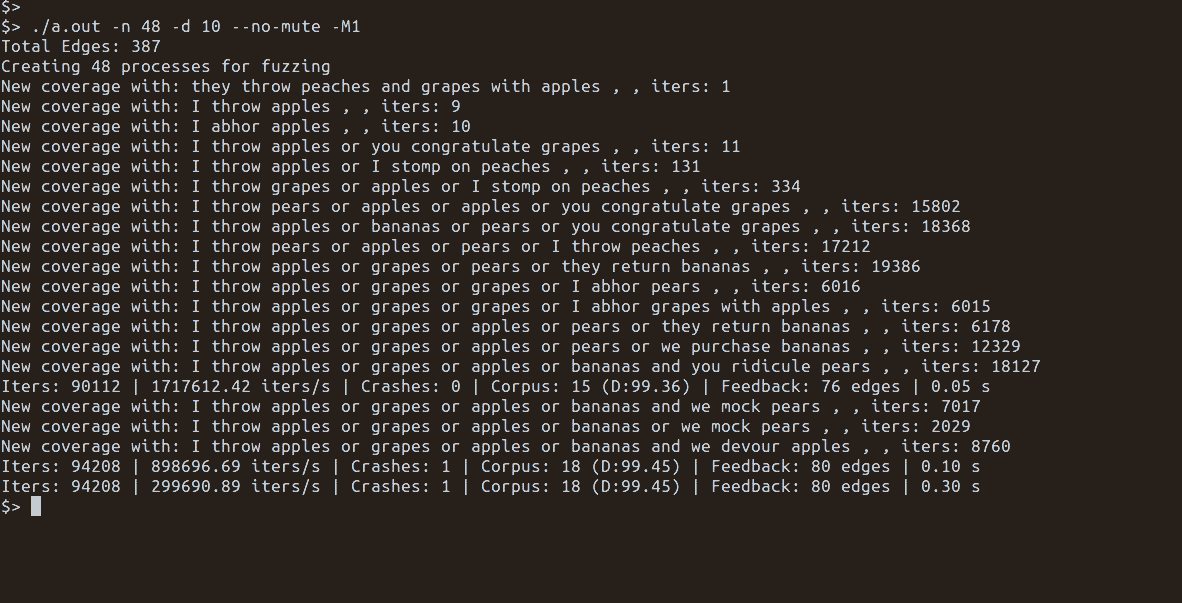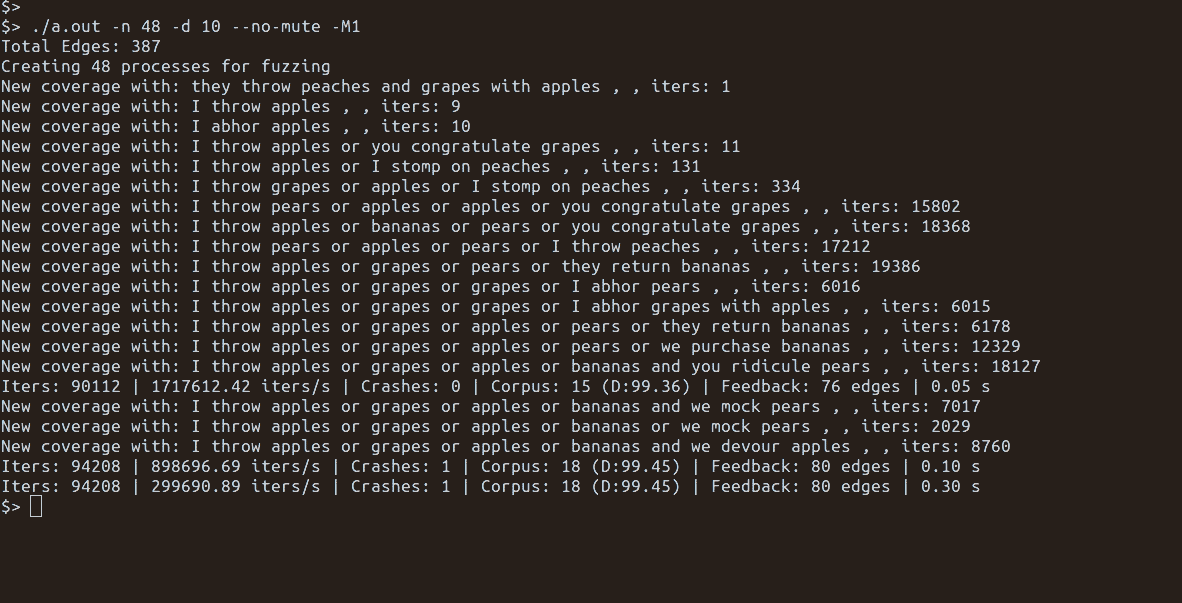
Doing feedback-driven fuzzing with grammars poses a different set of problems than pure mutational-based fuzzing. This blog post focuses on the corpus and mutation aspects of feedback-driven fuzzing.

Questions

What do you store in the corpus?

Storing only the generated data throws away knowledge of the structure, but not storing the generated data means you need to regenerate derivative inputs from scratch.

How Do You Reuse Structural Knowledge of Previous Inputs?

This hinges largely on the limitations of how previous inputs are stored in the corpus.

On one end of the spectrum, if you only store the generated data, you cannot use the structural knowledge about that input that existed when it was created. You may be able to store start/end offsets of the data that each rule generated, but this method falls apart when you’re working non-static (dynamic) grammars.

On the other end, if you have full knowledge about how an input was generated, you should be able to modify the decisions used during its creation to create a valid, but mutated, descendant of an input.

Grammar-specific Corpus

For resmack, I wanted to store each item in the corpus in a way that preserved the tree structure of the decisions used when data was generated by the grammar.

For example, the grammar below defines a run-on sentence. The zero-based line numbers indicate the rule indices, which will be used later:

0
1
2
3
4
5
6

run_on_sentence: <sentence> | <sentence> <conjunction> <run_on_sentence>
sentence: <subject> <verb> <fruit_list>
fruit_list: <fruit> | <fruit> <conjunction> <fruit_list>
subject: I | we | you
verb: eat | throw | stomp on | demolish
fruit: apples | bananas | pears | watermelon
conjunction: and | or

The sentence

I eat apples and bananas or we throw watermelon

Would be represented by the tree:

To preserve the decisions used at each junction in the tree, I found it worked well to save the full state of the pseudo-random number generator (PRNG) for each rule that was generated.

Implementing the same grammar as above in resmack would produce this metadata saved in the corpus:

Corpus Metadata:
  ...
  num_entries: 1
  entry[0]:
    ...
    item_header:
      num_states: 16
        state[ 0]: ... rule_idx: 0 "run_on_sentence" rand_state: ebe8df8d|fa44b3ba|6be3539c|f28d3079
        state[ 1]: ... rule_idx: 1 "sentence"        rand_state: e3215c4e|7a4f3fab|096cf811|4c1e1846
        state[ 2]: ... rule_idx: 3 "subject"         rand_state: e3215c4e|7a4f3fab|096cf811|4c1e1846
        state[ 3]: ... rule_idx: 4 "verb"            rand_state: d5707ba3|90029bf4|7432f25f|893f69b2
        state[ 4]: ... rule_idx: 2 "fruit_list"      rand_state: cc4d89e5|31401208|a47561fc|ef9230c9
		state[ 5]: ... rule_idx: 5 "fruit"           rand_state: 129fab24|5978fa11|e81cf819|91160ef6
        state[ 6]: ... rule_idx: 6 "conjunction"     rand_state: daf15fc3|a3fba92c|0b77713d|77a73e43
        state[ 7]: ... rule_idx: 2 "fruit_list"      rand_state: 0eadc8ac|727d87d2|26d476fe|e4bb7ea2
        state[ 8]: ... rule_idx: 5 "fruit"           rand_state: 0eadc8ac|727d87d2|26d476fe|e4bb7ea2
        state[ 9]: ... rule_idx: 6 "conjunction"     rand_state: 986b31dc|5a043980|d3761a52|37cb84b6
        state[10]: ... rule_idx: 0 "run_on_sentence" rand_state: f5a48cea|1119120e|436e2b8e|7de9b36e
        state[11]: ... rule_idx: 1 "sentence"        rand_state: 99542d8a|a7d3b56a|84eebb64|850b0367
        state[12]: ... rule_idx: 3 "subject"         rand_state: 99542d8a|a7d3b56a|84eebb64|850b0367
        state[13]: ... rule_idx: 4 "verb"            rand_state: bb8c9b87|ba692384|bad042ee|c5b06916
        state[14]: ... rule_idx: 2 "fruit_list"      rand_state: c455d115|bb35faed|d31bd169|ca5493fe
        state[15]: ... rule_idx: 5 "fruit"           rand_state: c455d115|bb35faed|d31bd169|ca5493fe

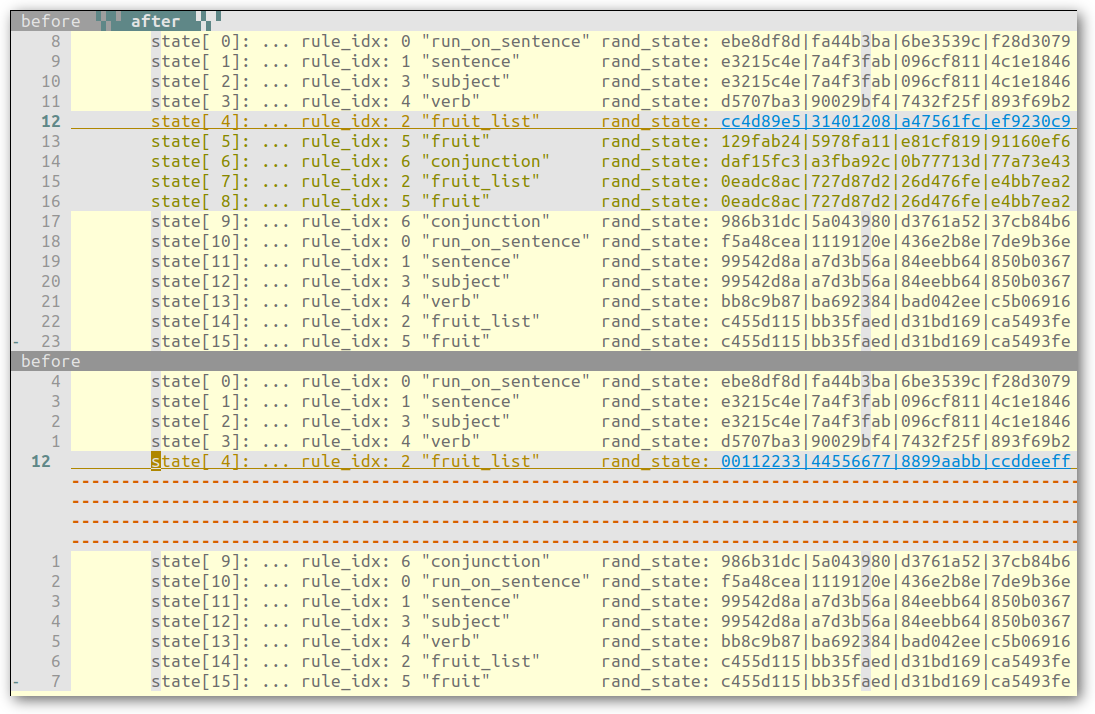
This is a portion of real data from my local, persisted corpus in resmack. The rule names were added for readability.

Notice how there are 16 PRNG states saved to generate this corpus item - one for each non-terminal node in the graph above (all nodes above the pink ones).

Saving the state of the PRNG at each rule generation results in a decision tree of sorts. Replaying the PRNG states in order at each rule generation will cause the same output to be generated.

On the flip side, modifying the persisted PRNG state at any node in the tree would:

1. invalidate all descendant nodes
   • new decisions will be made, but we don’t know what they are yet
2. cause that portion of the generated data to change

Mutating Grammar Decisions

Suppose I wanted to change the fruit_list value in the first sentence to something other than apples and bananas:

I eat apples and bananas or we throw watermelon
I eat ?????????????????? or we throw watermelon

This could be accomplished by changing the saved PRNG state values for that rule generation:

Note The image above is for illustration purposes only. The actual resmack corpus is a single binary file, not text-based like above.

Which would create the following tree:

Replaying the newly mutated saved state then yields a similar sentence, except it now has a new fruit list:

I eat watermelon or we throw watermelon

Crossover

The same technique can also be used to crossover multiple inputs in the corpus by swapping PRNG states for the same rules. For example, the PRNG state for a different corpus item’s fruit_list in the first sentence could overwrite the fruit_list PRNG state from another corpus item:

Remarks

PRNG Space Requirements

Due to the random number generator that I am using (Xoshiro128**), four 32-bit integers are used to track the PRNG’s state. The number of integers required could be reduced if a different random number generator algorithm was used.

Inefficiencies With Small Inputs

It is possible that a large number of PRNG states would be required to generate a very small input. The worst case would be one PRNG state being required for 0-1 bytes in the input.

For my use cases, this is an acceptable tradeoff since my primary targets will be generating much more than 16 bytes per rule.